System design requires that components supply pressure adjusted so that the operating envelope encompasses the worst case force-speed operating point. An infinite number of combinations exists that will accomplish this, so some other strategies must be applied to reduce the number of possibilities.
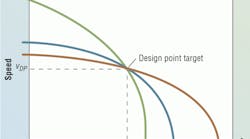
The first drawing shows three possible system designs, each of which just passes through the force-speed design point target. The low pressure drop strategy (shown in green) results in low power loss in the valve at the operating point; it is used in most conventional and on-off control systems. But it produces a very high slew speed and often becomes limited by pump output at low loads. This is undesirable in most servo systems because if the pump limits speed, then a small and undesirable shock usually occurs as the target position is approached, and the servo loop recovers control. The valve is not in control the entire time that the pump limits speed, and the system is running in open loop.
The high-pressure drop strategy, (shown in red), normally is undesirable for that reason alone. But to its advantage, valves tend to be smaller, potentially reducing system cost. Also, speed is fairly constant over a large load force change, even when operated in a non-closed loop configuration.
On the other hand, the optimal design strategy (the blue curve) should be applied whenever it can. It provides the best control, the lowest pressure for a given load, and will deliver maximum power to the load when the system is operated at the design point target force and speed.
Aiming for optimal design
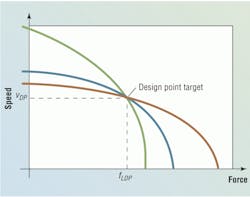
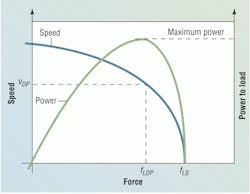
The concept of optimal design is suggested in the second drawing. If we draw the speed-force operating envelope for a given system (one quadrant is displayed just to keep it simple), but then add a second vertical axis for the power to the load, the two curves shown are the result. If the actuator is operated at zero load force, no power will be applied to the load. Also, if the system operates at stall condition, no power will be delivered to the load. However, at all other load points between zero and stall, the power to the load is not zero. Logically, then, a unique point exists where the load power is maximized.
This can be derived mathematically by solving for the load power term, then differentiating and setting the derivative equal to zero. When solving for maximum power transfer, we learn that when the stall force is 11⁄2 times the design point force, it will be where maximum power to the load prevails. The control in such a system is excellent; proper sizing strategy has been employed, and, coincidently, the minimum possible pressure will have been found to work the load.
However, the point of maximum power to the load is not the point of maximum efficiency. Curiously, the efficiency always works out to 67% at the design point and increases as load force approaches the stall condition. It goes to 100% right at stall, an interesting, but useless fact.
An electrical analogy
In contrast, electrical systems engineers apply maximum power transfer strategy to electrical actuation. The process is called impedance matching, but because of the linear nature of Ohm’s law, the efficiency is only 50%. That means that when you have your home stereo system operating with an 8-V speaker connected to your amplifier with 8-V output impedance, and you are pumping out 50 W to your speaker, your amplifier is also consuming 50 W. It will get hot. If you had a hydraulic servovalve driving your speaker, you could deliver, say, 50 hp to your speaker, but you would be consuming only 25 hp in your valve, however, the audio volume might be a bit excessive!
Handbook introduces cylinder control
The textbook contains 220 pages and sells for $59.95. To order, visit our Bookstore. Print the PDF order form, fill it out, and mail, fax, or e-mail it to us.