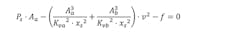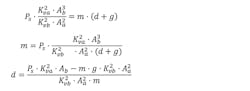In the last installment of “Motion Control”, the final recommended step in sizing a cylinder was checking for cavitation conditions. Cavitation occurs when the pressure in the cylinder drops below atmospheric pressure, so gasses trapped in the oil expand rapidly. Cavitation can damage the cylinder, pitting the walls and cap or degrading seals. Cavitation also will affect control, because the hydraulic motion controller can’t reduce the pressure to zero or below.
It is easy to tell when a cylinder is cavitating by the sound. Cavitation normally occurs on the cap side of the piston when it is extending quickly and attempting to stop an over-running load. Cavitation can also occur when the rod is pointing down with a heavy tensile load on the end—a common situation in presses. The problem is how to determine if the hydraulic cylinder, load, and motion profile will cause cavitation.
Detour: My First Experience with Cavitation
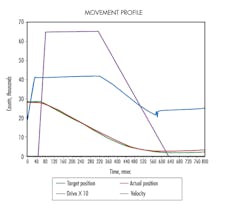
My first practical experience with cavitation occurred in 1989. A customer was trying to accelerate a heavy load about 26 in. in approximately 750 msec. The top target speed was 60 in./sec. We could hear the sounds of cavitation, but we didn’t know what it was. Sometimes O-rings were sucked into the oil and were later found in the filter. The motion controller was blamed for not getting the load to the final position quickly. The load would approach a command position, get close, then stall or even back up. I jury-rigged a system to record the motion and control output. The data was sent to a laptop running Lotus Symphony using x-modem. The data was saved, then printed out on a dot-matrix color printer. This was the first application where I recorded the data on plots.
The plots showed that the controller was providing a positive voltage to extend to the command position, but the load was not moving for many time-wasting milliseconds before finally moving to position. So now I pointed at the hydraulic guys and asked, “Why does a positive signal not move in the positive direction?” This was clearly a hydraulic problem.
After much debate, the possibility of cavitation was brought up. We were much better prepared on the next trip. Pressure sensors were installed on both ends of the cylinder, and an oscilloscope captured the pressure data. During a rapid move, the scope captured the voltage output from the pressure sensors. The voltage for the pressure sensor on the cap end of the piston dropped to zero, showing that the cylinder was cavitating.
The suggestion was to use a valve with a 2:1 asymmetrical spool. Finding a big valve (90+ gpm) with an asymmetrical spool was not easy. Instead, two Moog 60-gpm servo valves with asymmetrical 2:1 spools were used in parallel to provide the required flow. At that time, the motion controller could produce ±100 mA output, so driving two servo valves was no problem. The 2:1 asymmetrical valve solution worked. I still have the paper printouts from that research.
Cavitation Calculations
Let’s begin with the VCCM equation in terms of force:
Where:
Ps is the supply pressure
Aa is the area of the cap side of the piston
Ab is the area of the rod side of the piston
Kva is the valve flow constant for the A port
Kvb is the valve flow constant for the B port
Xs is the spool position, −1 to 1. −1 is full flow to the B port (retract), and 1 is full flow to the A port (extend)
v is the piston velocity
Cavitation occurs at some point when the fluid pressure drops below atmospheric pressure. We also know that the pressure on the side that is doing the braking must resist with enough force to slow down the load at the desired deceleration rate. Two equations are necessary.
The first is the equation for when the pressure in the cap-end chamber is less than atmospheric. At this point, I asked myself, “What should the zero-reference point be? Should it be absolute or one atmosphere?” The supply pressure for the VCCM equation is absolute, so the following calculations assume cavitation will occur at 0 psia. If this is the case, the term of the above VCCM equation that determines the force on the cap side of the piston is:
Divide by the area of the cap side to get the equation in terms of pressure:
Note that cavitation will occur a little above 0 psia.
The second equation also comes from the VCCM equation. It deals with the resistive force needed decelerate the load and the force generated by the load. The term on the left side is the force resisting or decelerating the load. The right side represents the force due to gravity plus the force required to decelerate the load:
The force can be broken into these two components:
Where:
m is the mass being decelerated
d is the deceleration rate
g is the acceleration due to gravity
We now have two equations and one unknown—the force. However, there is also the velocity, v, and the spool position, xs. We can see that that v2/xs2 is common to both equations, so by substitution, this term can be removed from both the equation for pressure on the cap side and the force on the rod side. Now these equations can be combined to solve for the braking force alone:
Now we can calculate the limits of the mass or deceleration:
If the tensile load exceeds the rod-end braking force, it’s easy to identify what can be modified to increase the braking force. System designers normally use symmetrical spools so that the flow constant for the A port (Kva) is the same as the flow constant on the B port (Kvb). However, it is easy to see that if the ratio of the flow constant on the A port is higher than that of the flow constant on the B port, the braking force can be increased. Because most valves have flow constants of 1:1 or 2:1, changing a symmetrical spool for a 2:1 spool will double the braking force. Another option is to decrease the rod diameter, thereby increasing the piston’s annular area. However, this is usually not an option on a press, for example, because the rod usually applies a high compressive force. The last solution is to increase the system pressure, but this may waste energy.
Summarizing Cavitation
So far, these calculations assume the supply pressure is absolute, so cavitation will occur if pressure in the cap-end of the cylinder drops to zero. To determine when this may happen, simply subtract the tank pressure from the supply pressure.
Avoiding cavitation must be considered when sizing cylinders and valves. It is easy to see there are many constraints, some of which conflict, so going through the calculations just once will not work. I have written a Python program that goes through all the steps to size cylinders and valves given parameters such as mass, move time, velocity limits, acceleration limits, system pressure, stall force, and minimum rod size. Sometimes a solution barely fails to meet all the criteria. In this case, my program makes suggestions like increasing system pressure, using the next size cylinder or valve, or reducing the maximum speed, maximum acceleration or deceleration. The designer must determine what compromises must be made, based on which performance criteria are most important to system operation.
Note: Much of the work presented here is based on theory published by Jack Johnson in his text Design of Electrohydraulic Systems For Industrial Motion Control. I then extended this theory using practical experience turning controls for hydraulic systems.
Peter Nachtwey is president of Delta Computer Systems Inc. and has more than 35 years of experience developing industrial control systems for hydraulic, electric, and pneumatic applications. In addition to leading Delta’s engineering and R&D programs, he contributes widely to the mathematical understanding of control theory, especially in fluid power systems.