To improve the productivity of machines, designers and integrators look for ways to make them run smoother. But often real-world conditions pose problems along the way. For example, sensor feedback signals can be noisy, or the valves that are selected could pose a problem, making precise hydraulic control difficult. When the real world doesn’t “behave” smoothly, what do you do?
If physical factors affect the smoothness or accuracy of machine operations, applying electronic filtering techniques can reduce output waste, accelerate production flow, and help machines last longer.
Simple electronic filtering
Just as hydraulic filters are used to remove unwanted particles from hydraulic oil, electrical filters made from discrete components or built into software or firmware are used to remove unwanted ‘noise’ from electronic signals. Filters can be of various types such as low pass, band pass or high pass, but this article will only cover the very basics of low pass filters that can easily be implemented in software in a PLC or motion controller. Most quality hydraulic motion controllers have built-in filters for different purposes.
Many hydraulic applications require a PLC or motion controller to control positions, speeds, pressures or forces. The control algorithms used for this purpose are dependent upon feedback devices that provide up-to-date information on the current state of the system so the controller can do precise closed-loop control. If the feedback signals transmit unwanted variations, then the control loop may produce unwanted variance in its output, which can cause a machine to exhibit unwanted motion. Many causes exist for noisy inputs coming from feedback devices, and some of the most prevalent ones are discussed in this article.
Noise or non-linearity
“Noise” can be true process noise, as in flow noise. But noise usually is not truly noise, but nonlinearities in the feedback system due to sample quantizing and jitter, discussed below. Most control systems are digital, so continuous analog data are converted to quantized digital numbers. The controllers use the digital information to estimate the true analog values. This is like using stairs to simulate a ramp. If there are many steps, then elevation change of each step is small. The more steps there are, the better the stairs approximate a true ramp, and the difference between the elevation anywhere along the stairs and the ramp become smaller and smaller.
Using higher-resolution feedback approximates the ramp in smaller steps. It is good to use the highest resolution feedback available to minimize the quantization error between the steps and the ramp. Older PLCs may have only 12- or 14-bit feedback, whereas most new control systems and motion controllers have 16-bit feedback and some have over-sampling which can deliver one or two additional bits of resolution.
Sample jitter
Another source of ‘noise’ is sample jitter. It is caused by sampling at irregular intervals and affects rate of change estimates of a sensor value, such as counts from an encoder. For instance, a conveyor may be moving at 10 counts every 10 msec. However, if a PLC samples every 10 msec on average, but has a sample jitter of 1 msec, then the time between samples may be 9, 10, or 11 msec. This can result in a change in the encoder counts of 9, 10, or 11 counts, which represents a variation of 10%. Many PLCs provide interrupts to service I/O devices but often disable the interrupts during computer housekeeping operations, which can cause encoder counts to be missed or misused. The best way to eliminate sample jitter is to read the encoder using a chip that can latch the counts at fixed intervals without the need for software, such as in a motion controller. It is also important to select a controller with a consistent or repeatable cycle time fast enough to read the latched values in time to process these values and produce valid control outputs.
Both quantizing and jitter make it difficult to compute the derivative of digital data. For example, encoder counts in motion control are used to compute a position and velocity, and in some cases they are also used to compute acceleration. Because the encoder position changes in steps, the computed velocity also changes in steps — and the acceleration changes in even bigger steps that are usually so large that the acceleration values calculated from the encoder data alone are not usable without some type of smoothing. A common question is how to compute linear or angular velocity from feedback provided by an encoder. This doesn’t look too hard at first, but complaints often arise that the computed velocity jumps around or isn’t stable. This really means that filtering must be applied.
The ideal low-pass filter
Low-pass filters are designed to eliminate high-frequency variations in signal data that would otherwise cause unintended fluctuations in control outputs. The ideal low-pass filter is one that eliminates all noise above a desired cutoff frequency. The-low pass filter doesn’t modify signal below the cutoff frequency and has no phase delay between the incoming signal and the filtered output.
In the reality of the physical world, however, the ideal filter doesn’t exist. Typically, the filtering effect of real-world filters starts to work gradually, and then more aggressively as the frequency approaches and exceeds the desired cutoff frequency. The filter usually causes some attenuation and phase delay starting before the cutoff frequency. The amount of signal attenuation and phase lag depends on the type of filters used.
Simple low-pass filters
The most common filter is the single-pole low-pass filter. The general form of the low pass filter is:
yn = A yn–1 + B xn (1)
Sometimes this formula is implemented as
yn = yn–1 + B (xn – yn–1) (2)
Where xn is the input to be filtered,
yn is the new filtered value,
yn–1 is the previous filtered value,
xn is the input value to be filtered, and
A and B are coefficients that are determined by the cutoff frequency or the filter time constant. The sum of A and B should equal 1.
A = e–∆t/t (3)
A= e–v∆t (4)
B = 1 – A (5)
Where ∆t is the update period,
t is the filter time constant, and
w is the cutoff (corner) frequency in radians/sec. Again, the sum of A and B should equal 1. Equation 5 ensures this is so.
Most people use Equation 2 and simply adjust Buntil they obtain the best results. Rather than thinking about what frequencies they want to eliminate, they choose a cutoff frequency and finally calculate B, which will usually be less than 0.5. The smaller the number, the smoother the output from the filter, but at the cost of signal phase delay. For a simple low-pass filter, the attenuation is -3 dB, or 0.707 of the original signal, and the phase delay is 45° at the cutoff frequency. The approximately 30% reduction at the cutoff frequency isn’t much, but the attenuation does increase that rapidly at higher frequencies. Plotted on a logarithmic scale, the attenuation is only -20 dB per decade — or a factor of 10 for every 10 times increase in the frequency.
Sometimes it is more convenient to think in terms of a time constant instead of a cutoff frequency. If the input signal makes a step change, it takes five time constants for the filtered value to be within 1% of the input signal.
Simple low-pass filters are easy to implement, but they aren’t very effective at filtering unless the filter time constant is relatively long or the corner frequency is relatively low. The corner frequency occurs where an input signal power is cut down by a factor of about 0.708 and is the frequency at which the signal power is attenuated by 3 dB. Typically, power is reported in dB. In a low-pass filter, the frequency region below the corner frequency is called the pass band, whereas the region above is called the stop band.
One drawback to low-pass filters is that the longer the filter time constant, or the lower the cutoff frequency, the larger the phase delay, which refers to the time lag in control signal propagation caused by the filtering process itself. Phase delay can cause problems with stability in motion control applications.
Cascading filters
Routing the filtered output of a simple low-pass filter to the input of another low-pass filter creates a cascading filter. Making a single-pole filter is easy, so it takes just a little more effort to make a two-pole filter by copying, pasting, and doing a little editing. The result is that the noise will be attenuated twice as fast than it is with a single-pole filter. The disadvantage of using two single-pole filters is that the phase delay increases even more rapidly. Each pole adds up to 90˚ of phase delay and will cause the amplitude of the signal to be attenuated by -3 dB at the cutoff frequency.
yn= A yn-1 + B • xn (6)
qn= A qn-1 + B • yn (7)
where qn is the new filtered output.
Two-pole low-pass filters
A two-pole low-pass filter is more effective at attenuating noise than a one-pole filter. It can function like two cascaded single-pole low-pass filters, but the calculations for the coefficients get a little more complicated because there are more of them. If you decide to go through this much effort, you should consider another improvement step and skip to a two-pole Butterworth filter.
Two-pole Butterworth filters
Compared to two-pole filters, two pole Butterworth filters have the advantage that gain stays closer to unity below the corner frequency. The gain for simple low-pass filters starts to roll off at lower frequencies sooner. Also, phase delay of the Butterworth filter is less than with the cascaded two-pole low-pass filter.
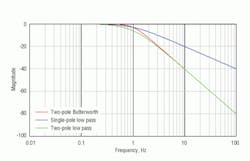
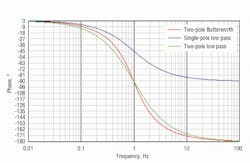
Figure 1 shows that each pole will add up to 90˚ of phase delay at higher frequencies. The Butterworth filter is a little better than the two-pole filter because its “knee” at the cutoff frequency is sharper and closer to that of an ideal low-pass filter. Therefore, the Butterworth filter will not affect the response below the cutoff frequency as much as the simple two-pole low-pass filter will. Plus, the Butterworth filter is better at filtering noise above the cutoff frequency.
Figure 2 shows that the two-pole filters attenuate the signal at a rate of -40 dB per decade instead of just -20 dB per decade of the single-pole filter.
A two-pole Butterworth filter can be implemented as:
z = 21/2/ 2
B0 = 1 - 2e-zv∆t × cos(zv∆t) + e–2zv∆t
A1 = 2e-zv∆t× cos(zv∆t)
A2 = -e-2zv∆t
yn = (A1yn-1) + (A2yn-2) + (B0xn)
The formulas for calculating the coefficients are derived using matched z transforms. Other methods can be used to calculate the coefficients, but the matched z transform method is the easiest to implement. Also, there are two A coefficients (A1 and A2), and the PLC must remember not only the last output (yn-1), but also the output before that (yn-2).
A comparison of filters
The corner frequency for each of the three filters, where the frequency response has an abrupt change in slope, is 1 Hz, or 2 π radians/sec.
Figure 1 illustrates how noise at each frequency is attenuated. This Bode plot shows that the slope to the right of 1 Hz is twice as steep for the two-pole filters. The noise at 10 Hz will be attenuated by a factor of 100 for the two-pole filters, but only by a factor of 10 for the single-pole filter. The phase lag for the two-pole filters is much more than the single-pole filter’s, Figure 2. However, in an application where the measured value is really only changing at 1 Hz or less, the delay between the filtered value and the true value is about 125 msec for the single-pole filter and 250 msec for the two-pole filters. These delays are fine if the filter value is being used for display, but they are too slow for most control applications. To reduce the delay, the cutoff frequency needs to be increased, but less noise reduction will result. Tradeoffs must always be made when using filters
Some PLCs have analog input cards and output cards that have simple low-pass filters built into them. This often eliminates the need to write a low-pass filter, but the options for the filter cutoff frequencies usually are limited. Some motion controllers have built-in filters that usually are more sophisticated and the sampling is done at a much higher control loop rate than what PLCs can achieve. Therefore, results are usually much better when using a motion controller.
For example, RMC motion controllers, Figure 3, from Delta Computer Systems Inc., contain built-in adjustable filtering parameters for position, velocity, acceleration, and even jerk (derivative of acceleration). In addition to input filtering, these controllers can also filter the control outputs in order to smooth the output to the electrohydraulic control valve. This can be helpful when the control output voltage to the valve is grassy (noisy).
Conclusion
Filtering techniques can help resolve real-world problems in hydraulic systems that would otherwise impact the rate and quality of machine output and increase maintenance costs. Some programmable motion controllers have built-in filtering functions to smooth the inputs and outputs of a motion control loop. But several different options for electronic filtering exist.
Basic low-pass filters have been presented here. The simple single-pole low-pass filter is relatively simple to implement and adjust to obtain desired results. The two-pole Butterworth filter needs to have some calculations done to correctly calculate the filter coefficients, but it reduces noise much better and has a sharper knee at the cutoff frequency and can produce even better results.
Peter Nachtwey is president of Delta Computer Systems Inc., Battle Ground, Wash. For more information on these topics, visit www.deltamotion.com.
Free book details motion control applications
Delta Computer Systems, Inc., Battle Ground, Wash., has released the second edition of its popular practical design guide authored by Delta president and chief motion control engineer Peter Nachtwey.
This 64-page guide covers 16 technical topics in fluid power motion control systems by combining theoretical and practical insights. Designers, mechanical and control systems engineers, fluid power technicians and others will benefit from this guide. The guide’s purpose is to be a resource when applying fluid closed-loop motion control systems in a wide variety of industrial and testing applications.
Topics covered include applications in different industries along with valuable tips related to open and closed loop motion control as they apply to component selection of accumulators, valves, and cylinders. Sensor resolution hints and tuning secrets round out the added information in the guide.
Click here to request a free copy, then enter your contact information and state “Design Guide” in the comments section. You may also call Delta at (360) 254-8688 or e-mail [email protected] to request a copy.