Download this article as a .PDF
Content has been updated as of Oct. 27, 2021.
Four different levels of analytical schematics of pump and motor models exist, arbitrarily numbered as Type 0 through Type 3, each one progressively more complex and more inclusive. Type 0 Models are ideal because they contain no losses. They are perfectly efficient, having 100% volumetric, mechanical, and overall efficiencies. They are referred to in industrial jargon as models for calculating the “theoretical” performance of pumps and motors. More-practical models include the theoretical imperfections encountered in the real world.
In analytical schematics, the idealized portions of the circuit are identified with an I inside the pump or motor symbol. The elements associated with losses are characterized as being external to the idealized elements. As more of the real performance of real machines is incorporated into the models with more and more theories, the model actually becomes more practical, not more theoretical, assuming, of course, that the modelers have applied the various theories correctly.
The Role of a Model
The purpose of mathematical models is to present a set of mathematical expressions that can be used to derive values for the variables that emulate the real machines they were designed to represent. Comparison to actual machine test data verifies the validity and usefulness of the model. The process of model verification with real data is called correlation, which provides a quantitative measure of the goodness-of-fit for the data.
A model can occur in at least two basic forms. The first is an analytical schematic, so called because the schematic is in a form that facilitates analysis of the circuit. That is, it facilitates the writing of descriptive equations. The second form is the set of describing equations themselves. The use of schematic models requires that the writer and user of the models agree on how, very specifically, the equations are to be written. Schematics are attractive to technical people because we like illustrations that convey details that mere equations sometimes cannot.
The equations themselves are always the more precise and unambiguous way to convey the exact nature of the model. The user will have less interpretation with the equations. However, equations present less opportunity for creative enhancements. On the other hand, analytical schematics facilitate non-mathematic interpretations better than equations do. The non-mathematical model will be covered here. However, the schematic models have undergone evolutionary improvements. They differ slightly from basic versions because details have been added.
Analyzing a Schematic
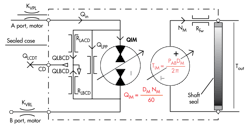
Figure 1 shows the analytical schematic for a Type-2 hydraulic motor. The mechanical shaft circuit is characterized as a hydraulic equivalent circuit—with torque analogous to pressure and shaft rotational speed analogous to hydraulic fluid flow. This figure contains a somewhat pictorial representation of the shaft seal and a pair of open triangles in the vicinity of the leakage orifices, RLACD and RLBCD, near the case drain port (CD).
The hydraulic displacement element is shown as a combination pump-motor. This is the most general configuration of any motor, or pump, for that matter. They will, depending upon circumstances, function as either a pump or a motor, because they are capable of converting power from hydraulic to mechanical and vice versa. Variable displacement is the default configuration, as shown.
A boundary rectangle encloses those elements in the analytical schematic that comprise the motor. It represents the physical case surrounding the active elements of the motor. The case also forms a repository for the outflow from some of the internal leakage paths. It is a sealed shell around the motor so that internal leakage does not drop on the floor and instead can be routed to tank.
Two internal leakage paths drain into the case. The lumped, equivalent, laminar orifices are labeled RLACD and RLBCD in Fig. 1, and the leakage components are labeled QLACD and QLBCD, respectively. Interpretation of the subscripts is “leak path from pressurized port A to case drain port” and “leak path from pressurized port B to case drain port,” respectively.
Visualize these pressure-port-to-case-drain port leak paths by imagining the internal workings of, say, an axial piston pump. Because of clearance between each piston and its bore, leakage must occur through all those clearances. In addition, it is common design practice to pressure balance the slippers, or shoes, riding on the swashplate. A small passage drilled through the center of the piston and slipper carries pressurized fluid to the slippers, providing, at once, pressure balance and required lubrication. But it, too, is an internal leak path.
The third leakage path is labeled QLPP, meaning the leakage path from port to port. Visualize this by looking at the clearance between the rotating cylinder block and the stationary port plate in an axial piston pump or motor, for example. The flow merely goes from the high-pressure port to the low-pressure port and is taken to tank in the case of the motor. It is not a contributor to the issues with the case and the shaft seal, so will be ignored for now.
High- or Low-Pressure Seal?
Figure 1 can be used to illustrate the need for—or the lack of the need for—a high-pressure shaft seal. Normally, any fluid collected in the case is carried back to tank via plumbing connected to the case drain port. It will do so at relatively low pressure, and the case pressure will be commensurately low. This is the point of the open arrows inside the motor envelope: The one downward-pointing open arrow carries leakage from the motor’s work ports and “releases it” to the internal cavity of the motor case. The other open arrow “points to” the external case drain port, and the implication is that it connects the case drain port to the internal cavity of the case. In this manner, internal leakage is eventually sent out the case drain port if the necessary external plumbing is provided. The analytical schematic helps illustrate both the problem and its solution.
However, a new argument is presented: What if the case drain port is blocked? Connecting the case drain plumbing is costly and is not necessary in all cases. Suppose the pressure of the motor’s Port A is high and Port B is low. Leakage will flow through RLACD to the case. With the case drain blocked, the only escape route will be backwards, through RLBCD! If the machine is relatively symmetrical—that is, if all piston to bore clearances are similar—then it stands to reason that the values of RLACD and RLBCD will be similar. Furthermore, if it takes high pressure to force leakage through the A side, then high pressure will be needed to drain off the leakage through RLBCD on the B side. This fluid joins the port-to-port leakage and is carried to tank on the low-pressure side.
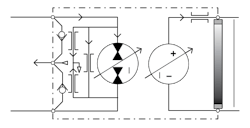
Check valves are often mounted integral with the motor body to relieve the case drain pressure without external case drain plumbing (Fig. 2). This strategy ensures that the case will always be relieved at the lower of the two port pressures. However, this does not ensure that a low-pressure shaft seal can be used—especially if the motor has a valve for speed and directional control. When in doubt, use high-pressure shaft seals or connect the case drain port to the reservoir with its own dedicated plumbing.
Assuming that the two leakage paths are similar in effective size, then the case drain pressure will settle to about one-half the pressure on the higher side if we also assume that the low pressure is at or nearly at tank pressure. Allowing for normal backpressure to tank, and imperfect symmetry in the internal clearances, the case drain pressure can be between 30% and 70% of supply pressure. Both the shaft seal and the physical case envelope must contain this pressure without rupture. This reality is easy to see when viewing the motor in its Type-2 analytical schematic form.